1. Обыкновенные дроби

1.1. Зачем нужны обыкновенные дроби?

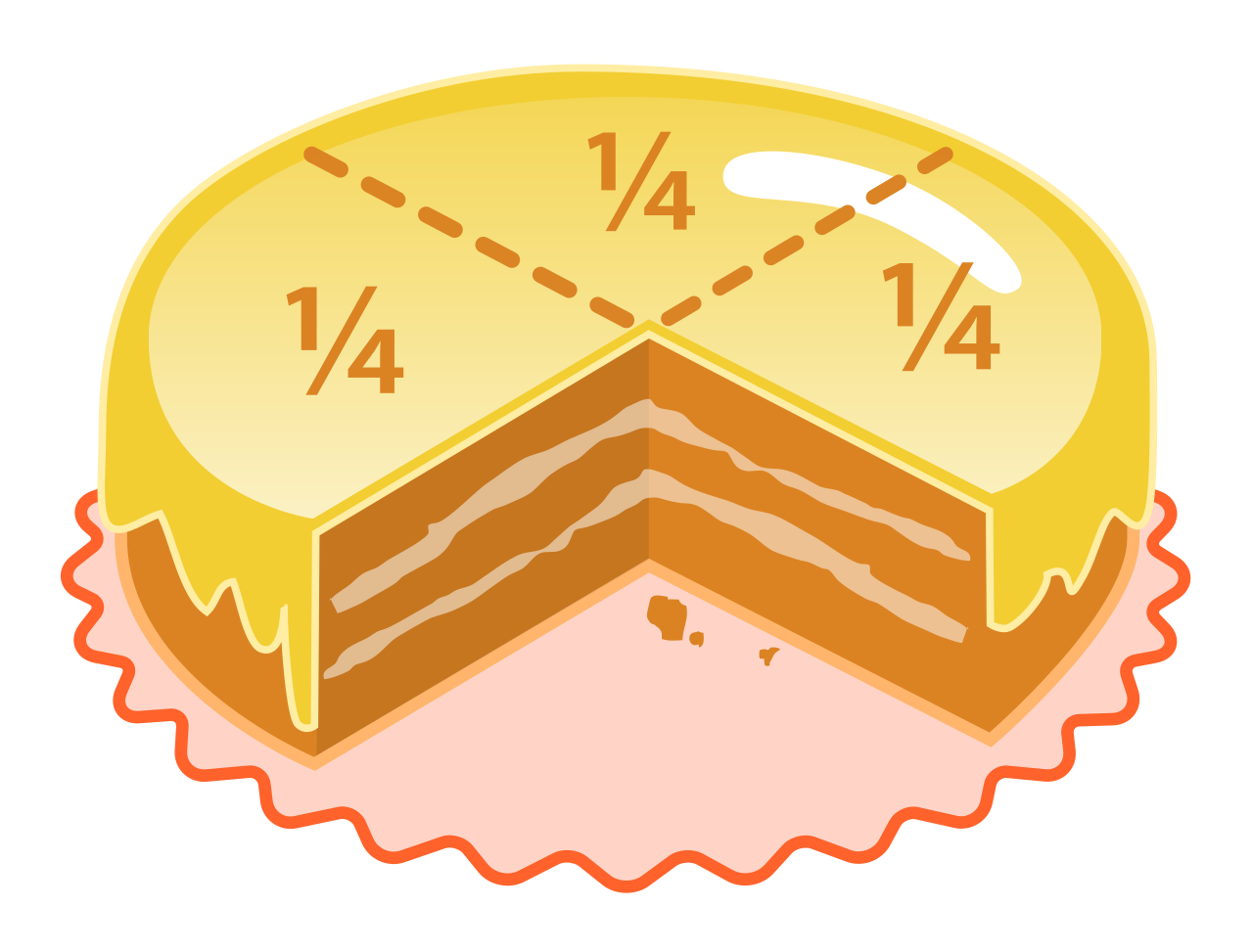
Например, представим, что у вас день рождения, и к вам пришли 4-ро друзей. Разделив торт среди них всех поровну, каждый получит «одну четвёртую торта» – \(\frac{1}{4}\). Вот вам и дроби в повседневной жизни :)

А вообще, это важная математическая абстракция.

1.2. Определение

Обыкновенная дробь (англ. Ordinary fractions) – это выражения вида \(\Large \frac{m}{n}\), где \(m\) и \(n\) – натуральные числа.

То есть, выражаясь математическим языком: \(m, n \in \mathbb{N}\).

Примечание

Символ \(\Large \in\) – обозначает принадлежность к какому-то множеству.

Например, утверждение «Все кошки (К) есть животные (Ж)» с помощью математической записи можно запистаь так: \(К \in Ж\) – «Кошки» являются элементом множества «Животные».

Где \(\Large \frac{m}{n} = \frac{числитель}{знаменатель}\)

число над чертой называется числителем, а число под чертой — знаменателем. Первый играет роль делимого, второй — делителя.

Обыкновенные дроби с целыми числителями и знаменателями образуют поле рациональных чисел.

Пример использования обыкновенной дроби:

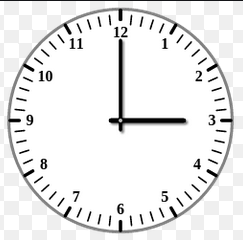
Допустим, сейчас 3 часа ночи. Какая часть суток прошла?

В сутках 24 часа, а прошло 3 часа из этих 24, то получается «три двадцатьчетвёртых» – \(\Large \frac{3}{24}\). А если сократить эту дробь на 3, то получим «одну восьмую» – \(\Large \frac{1}{8}\). Прошла \(\Large \frac{1}{8}\) суток.

1.3. Типы дробей

Обыкновенные дроби бывают нескольких видов:

1. Правильные

   • \(числитель < знаменатель\).
   • Например числа: \(\frac{1}{2}, \frac{3}{4}, \frac{1}{8}\) и так далее.

2. Неправильные

   • \(числитель > знаменатель\)
   • Например числа: \(\frac{10}{9}, \frac{5}{3}, \frac{14}{3}\) и так далее.

3. Смешанные

   • Дроби вида \(a + \frac{b}{c}\) называют смешанными. То есть здесь выделяется целая часть.

     • Пример: \(1 + \frac{1}{9}\).

   • Как правило, в записи этих чисел знак «+» опускают и пишут \(a\frac{b}{c}\).

     • Пример: \(1\frac{1}{9}\).

   • Всякую смешанную дробь можно представить в виде обыкновенной: \(a + \frac{b}{c} = \frac{ac + b}{c}\).

     • Пример: \(1 + \frac{1}{9} = \frac{1 \cdot 9 + 1}{9} = \frac{10}{9}\).

   • Например числа: \(1\frac{1}{9}, 7\frac{3}{4}\) и так далее.

1.4. Основное свойство дроби

При умножении или делении числителя и знаменателя на одно и то же число – значение дроби не меняется.

\[\Large \frac{a}{b} = \frac{a \cdot c}{b \cdot c}\]

1.5. Сложение и вычитание дробей

1.5.1. С одинаковыми знаменателями

Если дроби имеют одинаковый знаменатель, то суммой/разностью этих дробей будет дробь, числитель которой равен сумме/разности числителей исходных дробей, а знаменатель равен исходному знаменателю.

\[\Large \frac{a}{c} \pm \frac{b}{c} = \frac{a \pm b}{c}\]

Примечание

Пример вычитания дробей. Найдите значение выражения: \(\large 4\frac{2}{3} - \frac{5}{3}\)

Решение:

1. Сначала представим в виде неправильной дроби дробь: \(\large 4\frac{2}{3}\)

   • \(\large 4\frac{2}{3} = \frac{4 \cdot 3 + 2}{3} = \frac{14}{3}\)

2. Теперь можем вычесть из одной дроби другую:

   • \(\large 4 \frac{2}{3} - \frac{5} {3} = \frac{14} {3} - \frac{5} {3} = \frac{9} {3} = 3\)

3. Ответ: \(\large 3\)

1.5.2. С разными знаменателями

Если дроби имеют разные знаменатели, то сначала нужно воспользоваться основным свойством дробей и привести их к общему знаменателю, а потом просто воспользоваться правилом сложения/вычитания дробей.

\[\Large \frac{a}{c} \pm \frac{b}{d} = \frac{a \cdot d \pm b \cdot c}{c \cdot d}\]

Примечание

Пример сложения дробей. Сложите дроби: \(\frac{2}{5} + \frac{3}{4}​\)

Решение:

1. Нам даны дроби с разными знаменателями, поэтому сначала приведем их к общему знаменателю.

   • \(\large \frac{2}{5} = \frac{2 \cdot 4}{5 \cdot 4} = \frac{8}{20}\)
   • \(\large \frac{3}{4} = \frac{3 \cdot 5}{4 \cdot 5} = \frac{15}{20}\)

2. Теперь, когда мы получили дроби с одинаковыми знаменателями, можем сложить их:

   • \(\large \frac{2}{5} + \frac{3}{4} = \frac{8}{20} + \frac{15}{20} = 1\frac{3}{20}\)

3. Ответ: \(\large 1\frac{3}{20}\)

Внимание

При сложении и вычитании смешанных чисел, можно отдельно сложить (вычесть) целые и дробные их части. Например, \(\large 2\frac{1}{6}+5\frac{5}{12}=(2+5)+\frac{2+5}{12}=7\frac{7}{12}\)

1.6. Умножение и деление дробей

1.6.1. Умножение

Произведение двух обыкновенных дробей есть дробь, числитель которой равен произведению числителей исходных дробей, а знаменатель произведению знаменателей исходных дробей.

\[\Large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d}\]

Примечание

Пример умножения дробей. Вычислим: \(\frac{3}{5} \cdot 2\frac{1}{4}​\)

Решение:

1. Сначала представим дробь \(\large 2\frac{1}{4}\) в виде неправильной:

   • \(\large 2\frac{1}{4} = \frac{9}{4}\)

2. Теперь перемножим одну дробь на другую:

   • \(\large \frac{3}{5} \cdot \frac{9}{4}​ = \frac{3 \cdot 9}{5 \cdot 4} = \frac{27}{20}\)

3. Выделим целую часть, если того требует задание:

   • \(\large \frac{27}{20} = 1\frac{7}{20}\)

4. Ответ:

   • \(\large 1\frac{7}{20}\)

1.6.2. Деление

Частное двух обыкновенных дробей равно произведению первой дроби на перевёрнутую вторую дробь.

\[\Large \frac{a}{b} : \frac{c}{d} = \frac{a \cdot d}{b \cdot c}\]

Внимание

При умножении и делении смешанных чисел необходимо представлять эти числа в виде обыкновенных дробей!

1.6.3. Прочие свойства

• Дроби \(\large \frac{a}{b} и \frac{b}{a}\) являются взаимно обратными. Произведение взаимно обратных дробей равно единице: \(\large \frac{a}{b} \cdot \frac{b}{a} = 1\)

1.7. Основные формулы

1. Сложение/вычитание дробей:

   • \(\Large \frac{a}{c} \pm \frac{b}{c} = \frac{a \pm b}{c}\)
   • \(\Large \frac{a}{c} \pm \frac{b}{d} = \frac{a \cdot d \pm b \cdot c}{c \cdot d}\)

2. Умножение/деление дробей:

   • \(\Large \frac{a}{c} \pm \frac{b}{d} = \frac{a \cdot d \pm b \cdot c}{c \cdot d}\)
   • \(\Large \frac{a}{b} : \frac{c}{d} = \frac{a \cdot d}{b \cdot c}\)

3. Взаимная обратность:

   • \(\Large \frac{a}{b} \cdot \frac{b}{a} = 1\)